[Fortran + Xfig] [php + svg] [Konvergenz]

Fraktal als Vektorgrafik

Manche Dinge sind einfach zu komplex, um sie von Hand zu machen, lassen sich aber auf ganz einfache Regeln zurückführen.
Ein Beispiel hierfür ist das Fraktal der Startseite www.Jachens.de.

Die Positionen jeder neuen Generation von Kreisen lässt sich per Rekursion aus ihren Müttern und Großmüttern ableiten.

Ein Weg, die errechnete Geometrie anzuzeigen, ist, direkt eine Scalable Vector Graphic zu schreiben, die von Browsern dargestellt wird und mittels Inkscape bearbeitet werden kann.

Die ursprüngliche Variante war noch in FORTRAN programmiert.

 

<?php
function genJachensFractal($level){
  /*
  Author: Dr. Arne Jachens
  Source: https://arne.jachens.de
  */
  global $Position,$Mother,$NoCircles,$Radius;
  $msg = "";
  
  /* no of cicles per level */
  $NoCircles[-1] = 0;
  $NoCircles[0] = 1;
  $NoCircles[1] = 4;
  for($n=2;$n<$level;$n++){
    $NoCircles[$n] = $NoCircles[$n-1]*3;
  } #n

  /* radii and distances of the cycles */
  $Radius[0] = 50;
  for($n=1;$n<$level;$n++){
    $Radius[$n] = 0.5*$Radius[$n-1];
    $step[$n] = 2.0*$Radius[$n-1];
    $msg.= $n." ".$NoCircles[$n]." ".$Radius[$n]."</br>\n";
  } #n

  $Position['x'] = array();
  $Position['y'] = array();
  $Mother = array();
 
  /* Positionen level=0 */
  $n=0;
  $Position['x'][$n] = 0.0;
  $Position['y'][$n] = 0.0;
  $Mother[0]=0;               #creation
  
  /* Positionen level>0 */
  $offset=0;
  for($n=1;$n<$level;$n++){
    /* loop over nodes of previous level */
    $offset = $offset + $NoCircles[$n-2];
    for($loop=0;$loop<$NoCircles[$n-1];$loop++){
      $thisMother = $offset+$loop;
      $x_Mother = $Position['x'][$thisMother];
      $y_Mother = $Position['y'][$thisMother];
      /* North */
      $x = $x_Mother ;
      $y = $y_Mother + $step[$n];
      test_position($x,$y,$thisMother);
      /* East */
      $x = $x_Mother + $step[$n];
      $y = $y_Mother;
      test_position($x,$y,$thisMother);
      /* South */
      $x = $x_Mother ;
      $y = $y_Mother - $step[$n];
      test_position($x,$y,$thisMother);
      /* West */
      $x = $x_Mother - $step[$n];
      $y = $y_Mother;
      test_position($x,$y,$thisMother);
    } #loop
  } #n
  return $msg;
}

/*%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%*/
function test_position($x,$y,$thisMother){
  global $Position,$Mother;
  $Grandma   = $Mother[$thisMother];
  $x_Mother  = $Position['x'][$thisMother];
  $y_Mother  = $Position['y'][$thisMother];
  $x_Grandma = $Position['x'][$Grandma];
  $y_Grandma = $Position['y'][$Grandma];
  $a = $x       -$x_Mother;
  $b = $y       -$y_Mother;
  $c = $x_Mother-$x_Grandma;
  $d = $y_Mother-$y_Grandma;
  /* not back to grandma */
  if(pow($a+$c,2)+pow($b+$d,2) > pow($c,2)+pow($d,2) ){
    array_push($Mother,$thisMother);
    array_push($Position['x'],$x);
    array_push($Position['y'],$y);
  } #fi
  return;
}

/*%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%*/
function writeSVG($level,$fill,$stroke,$fracFile){
  global $Position,$Mother,$NoCircles,$Radius;

  /* scaling */
  $imgWidth = 8*$Radius[0];

  /* stroke-width reduction */
  for($n=0;$n<$level;$n++){
    $strokeWidth[$n] = 0.02*$Radius[$n];
  } #n
  
  $fracSVG = "";
  /* rectangles as  connectors */
  $offset=0;
  for($n=1;$n<$level;$n++){
    $offset = $offset + $NoCircles[$n-1];
    /* loop over nodes of this level */
    for($loop=0;$loop<$NoCircles[$n];$loop++){
      $x_tochter = 0.5*$imgWidth + $Position['x'][$offset+$loop];
      $y_tochter = 0.5*$imgWidth + $Position['y'][$offset+$loop];
      $x_Mother  = 0.5*$imgWidth + $Position['x'][$Mother[$offset+$loop]];
      $y_Mother  = 0.5*$imgWidth + $Position['y'][$Mother[$offset+$loop]];
      $x = min($x_tochter,$x_Mother);
      $y = min($y_tochter,$y_Mother);
      if(abs($x_tochter-$x_Mother)<1E-6){
	/*vertical */
	$width  = $Radius[$n];
	$x = $x-0.5*$width;
	$height = abs($y_tochter-$y_Mother);
      }else{
	/* horizontal */
	$width  = abs($x_tochter-$x_Mother);
	$height = $Radius[$n];
	$y = $y-0.5*$height;
      }
      $fracSVG.= "<rect x='".$x."' y='".$y."' width='".$width."' height='".$height."' stroke-width='".$strokeWidth[$n]."' class='fracRect' />\n";
    } #loop
  } #n
 
  
  /* circles */
  $offset=0;
  for($n=0;$n<$level;$n++){
    $offset = $offset + $NoCircles[$n-1];
    /* loop over nodes of this level */
    for($loop=0;$loop<$NoCircles[$n];$loop++){
      $xc = 0.5*$imgWidth + $Position['x'][$offset+$loop];
      $yc = 0.5*$imgWidth + $Position['y'][$offset+$loop];
      $r = $Radius[$n];
      $fracSVG.= "<circle cx='".$xc."' cy='".$yc."' r='".$r."' stroke-width='".$strokeWidth[$n]."' class='fracCirc' />\n";
    } #loop
  } #n
  
  $svgHead = "<?xml version='1.0' encoding='UTF-8' standalone='no'?>\n";
  $svgHead.= "<svg xmlns='http://www.w3.org/2000/svg' \n";
  $svgHead.= "   xmlns:dc='http://purl.org/dc/elements/1.1/' \n";
  $svgHead.= "   xmlns:cc='http://creativecommons.org/ns#' \n";
  $svgHead.= "   xmlns:rdf='http://www.w3.org/1999/02/22-rdf-syntax-ns#' \n";
  $svgHead.= "   viewBox='0 0 ".$imgWidth." ".$imgWidth."'>\n";
  $svgHead.= "<defs>\n";
  $svgHead.= "  <style type='text/css'><![CDATA[\n";
  $svgHead.= "    .fracCirc {\n";
  $svgHead.= "      stroke: ".$stroke.";\n";
  $svgHead.= "      fill: ".$fill.";\n";
  $svgHead.= "    }\n";
  $svgHead.= "    .fracRect {\n";
  $svgHead.= "      stroke: ".$stroke.";\n";
  $svgHead.= "      fill: ".$fill.";\n";
  $svgHead.= "    }\n";
  $svgHead.= " ]]></style>\n";
  $svgHead.= "</defs>\n";
  /*
  $svgHead.= "<metadata>\n";
  $svgHead.= "   <rdf:RDF>\n";
  $svgHead.= "      <cc:Work>\n";
  $svgHead.= "        <dc:format>image/svg+xml</dc:format>\n";
  $svgHead.= "        <dc:type\n";
  $svgHead.= "           rdf:resource='http://purl.org/dc/dcmitype/StillImage' />\n";
  $svgHead.= "        <dc:title>Jachens Logo</dc:title>\n";
  $svgHead.= "        <dc:creator>\n";
  $svgHead.= "          <cc:Agent>\n";
  $svgHead.= "            <dc:title>Dr. Arne Jachens</dc:title>\n";
  $svgHead.= "          </cc:Agent>\n";
  $svgHead.= "        </dc:creator>\n";
  $svgHead.= "        <dc:publisher>\n";
  $svgHead.= "          <cc:Agent>\n";
  $svgHead.= "            <dc:title />\n";
  $svgHead.= "          </cc:Agent>\n";
  $svgHead.= "        </dc:publisher>\n";
  $svgHead.= "        <dc:source>https://www.jachens.de</dc:source>\n";
  $svgHead.= "        <cc:license\n";
  $svgHead.= "           rdf:resource='' />\n";
  $svgHead.= "      </cc:Work>\n";
  $svgHead.= "    </rdf:RDF>\n";
  $svgHead.= "</metadata>\n";
  */
  $svgFoot = "\n</svg>";

  $fid = fopen($fracFile,"w");
  fputs($fid,$svgHead);
  fputs($fid,$fracSVG);
  fputs($fid,$svgFoot);
  fclose($fid);
  $msg = "<p>Fractal written to:</br>\n".$fracFile."</p>";
  return $msg;
}

?>

 

Konvergenz der Arme des Franktals

Um die Ausgangsfrage zu beantworten, ob die Arme des Fraktals sich irgendwann berühren:
Nehmen wir 2 markante Punkte, indem wir einmal eine Generation nach rechts und dann nach oben laufen, und einmal eine Generation nach oben und dann nach rechts laufen.
In diesem Beispiel ist der Abstand der Tochter von der Mutter gleich dem doppelten Radius der Mutter. Und der Radius der Tochter ist halb so groß wie der der Mutter.

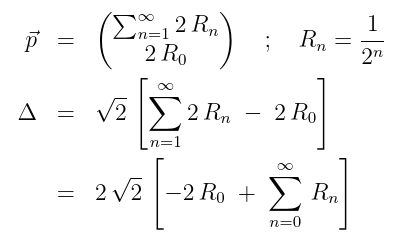
Die Punkte liegen symmetisch und tauschen einfach ihre Koordinaten; dadurch ergibt sich bei der Abstandsberechnung die Wurzel aus 2.

Der Ausdruck in den eckigen Klammern lässt sich auf die geometrische Reihe zurückführen und mit deren Grenzwert wird der Ausdruck in den eckigen Klammern Null.

Mit anderen Worten: Für jeden endlichen Detailierungsgrad bleibt der Abstand der Fraktalarme infenitesimal klein.