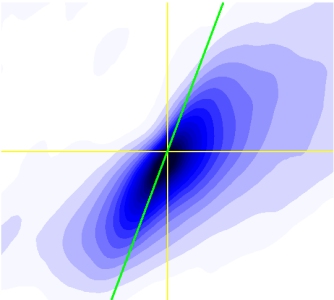
PlotData3D.m
Im Rahmen meiner Dissertation hatte ich mehrere Datensätze, bestehend aus fortlaufend nummerierten Datein, aus denen ich Contourplots generieren und diese zu einem Film kompositionieren wollte.
pfad = strcat("./")
dataset = strcat("VU")
%dataset = strcat("UU")
%spezifische Anpassung des Plots
if (dataset=="UU")
mytitle=["UU"];
levels=[-4 -2 0 +2 +4];
%Farbdeklarationen rot -- blau
mycolors(64:-1:33,1:3) =transpose([linspace(1,1,32);linspace(0,1,32);linspace(0,1,32);]);
mycolors(1:32,1:3) =transpose([linspace(0,1,32);linspace(0,1,32);linspace(1,1,32);]);
elseif (dataset=="VU")
mytitle=["VU"];
levels=[-8 -6 -4 -2 0];
%Farbdeklarationen weiss -- blau
mycolors(01:32,1:3) =[linspace(0,0,32);linspace(0,0,32);linspace(0.2,1,32);];
mycolors(33:64,1:3) =[linspace(0,1,32);linspace(0,1,32);linspace(1,1,32);];
end %if
colormap(mycolors);
for i = 1:10
%Einlesen der Daten
dateiname = strcat(sprintf(pfad),sprintf(dataset),"_",sprintf("%03d",i),".dat")
[x,y,z]=textread(dateiname,"%f %f %f ");
%Generierung des Gitters
XX = linspace(min(x),max(x),101);
YY = linspace(min(y),max(y),101);
[GridX,GridY] = meshgrid(XX,YY);
%Interpolation der Daten
GridZ = griddata(xx,yy,w,GridXX,GridYY,"cubic");
%Contourplot
[c,h]=contourf(GridX,GridY,GridZ,levels);
set(h,"LineStyle","none");
set(gca,"FontSize",20);
set(0,"DefaultAxesFontSize",14);
set(0,"DefaultAxesFontWeight","bold");
colorbar("vert");
title(mytitle);
xlabel ("XX")
ylabel ("YY")
axis([0,180,0,180]);
axis equal;
set(gca,"xtick",[0 30 60 90 120 150 180])
set(gca,"ytick",[0 30 60 90 120 150 180])
%Koordinatenkreuz
x0=[0.,180.];
y0=[90.,90.];
x1=[90.,90.];
y1=[0.,180.];
hold on;
plot(x0,y0,"-k","LineWidth",1);
plot(x1,y1,"-k","LineWidth",1);
hold off;
%Bilder speichern
bild1 =strcat(sprintf(pfad),sprintf(dataset),"_",sprintf("%03d",i),".png")
bild2 =strcat(sprintf(pfad),sprintf(dataset),"_",sprintf("%03d",i),".eps")
bild3 =strcat(sprintf(pfad),sprintf(dataset),"_",sprintf("%03d",i),".pdf")
print ("-dpng",bild1)
set(gcf, "PaperPositionMode", "manual");
set(gcf, "PaperPosition", [1 5 18.0 18.0]);
set(gcf, "PaperType", "A4");
print ("-depsc2", bild2);
print ("-dpdf", bild3);
end %i
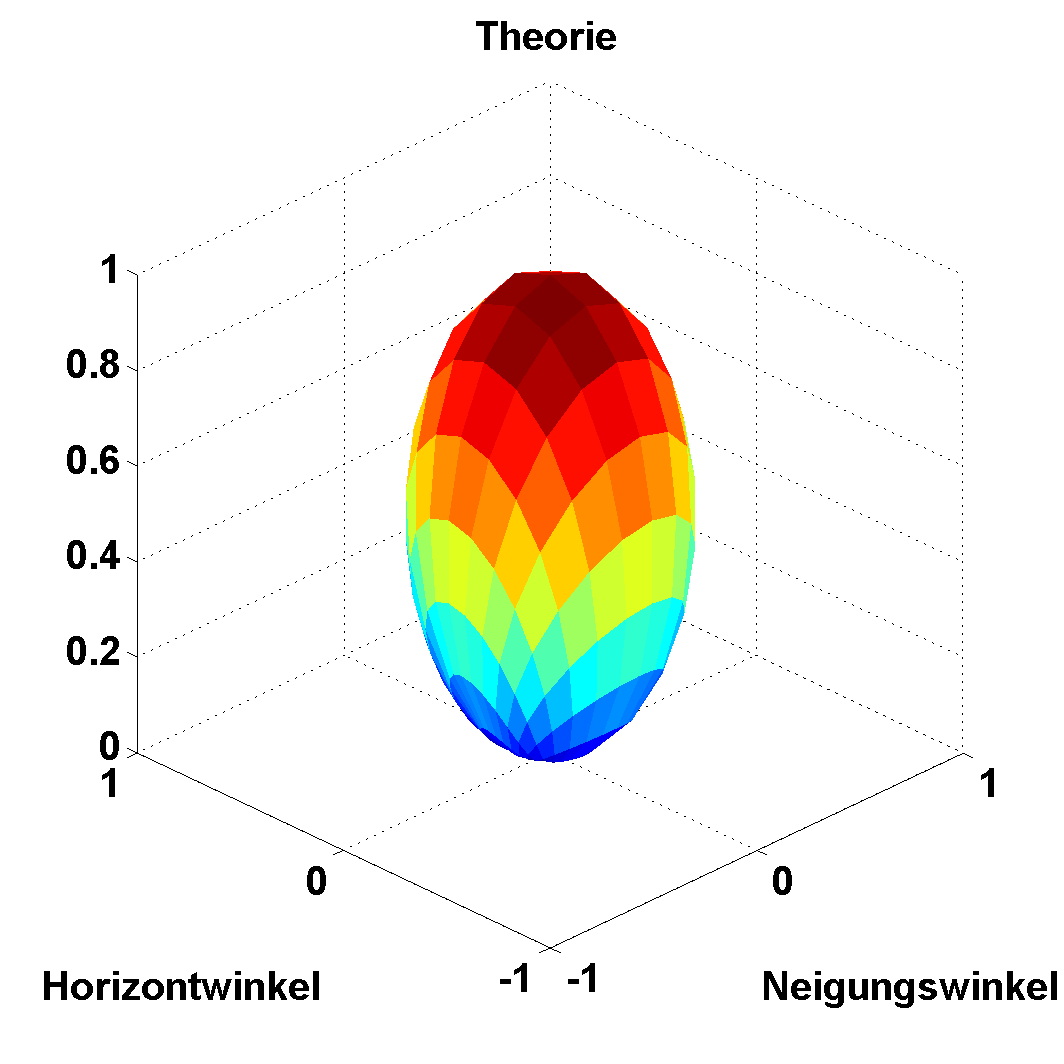
BallPlot.m
Um richtungsabhängige Informationen darzustellen, kann man eine Kugel mit diesen Daten skalieren und erhält so ein deformiertes Ei.
Die Beispieldatei enthaelt in Spalte 1 und 2 die Winkel von 0 bis 180, Spalte 3 und 4 die zu vergleichenden Datensätze.
clear;
pfad = strcat("./")
PI=3.14159;
%field = strcat("Variable1")
%field = strcat("Variable2")
field = strcat("Ball")
N=19;
%Einlesen der Felder
dateiname = strcat(sprintf(pfad),"Data_V1_V2.dat")
[Theta,phi,V1,V2]=textread(dateiname,"%f %f %f %f ");
dim=size(Theta)
Tspace = linspace(0,180,N);
Fspace = linspace(0,180,N);
[GridT,GridF] = meshgrid(Tspace,Fspace);
if (field=="V1")
GridI=griddata(Theta,phi,V1,GridT,GridF,"cubic");
mytitle=["Variable1"];
maxV=max(V1);
elseif (field=="V2")
GridI=griddata(Theta,phi,V2,GridT,GridF,"cubic");
mytitle=["Variable2"];
maxV=max(V2);
end
xx=zeros(N,N);
yy=zeros(N,N);
zz=zeros(N,N);
for i=1:N
for j=1:N
%Winkelwerte
Theta_tmp=(i-1)*180/(N-1);
phi_tmp=(j-1)*180/(N-1);
%Umrechnung der Winkel in Richtungsvektoren
xx(i,j)=cos(phi_tmp*PI/180);
yy(i,j)=cos(Theta_tmp*PI/180)*sin(phi_tmp*PI/180);
zz(i,j)=sin(Theta_tmp*PI/180)*sin(phi_tmp*PI/180);
if (field=="Ball")
% theoretischer Referenzwert, Zenit: (0,0,1)
xr(i,j)=xx(i,j)*zz(i,j);
yr(i,j)=yy(i,j)*zz(i,j);
zr(i,j)=zz(i,j)*zz(i,j);
mytitle=["homogene Verteilung"];
else
%Skalierung mit gemessener Intensitaet
x(i,j)=xx(i,j)*GridI(i,j);
y(i,j)=yy(i,j)*GridI(i,j);
z(i,j)=zz(i,j)*GridI(i,j);
mytitle=field;
end
end %j
end %i
%Umrechnung der Winkel in Richtungsvektoren
scale=1;
for i=1:dim
xxx(i)=cos(phi(i)*PI/180);
yyy(i)=cos(Theta(i)*PI/180)*sin(phi(i)*PI/180);
zzz(i)=sin(Theta(i)*PI/180)*sin(phi(i)*PI/180);
xxx(i)=xxx(i)*(scale*V2(i));
yyy(i)=yyy(i)*(scale*V2(i));
zzz(i)=zzz(i)*(scale*V2(i));
end %i
if (field=="Ball")
%Kegel
h=surf(xr,yr,zr);
%Halbkugel
%h=surf(xx,yy,zz);
else
maxV= z(10,10)
h=surf(x/maxV,y/maxV,z/maxV);
end
%Blickrichtung
az = -45;
el = 30;
view(az, el);
set(h,"LineStyle","none");
set(0,"DefaultAxesFontSize",20);
set(0,"DefaultAxesFontWeight","bold");
axis([-1,1, -1,1]);
%caxis([0 1]);
%colorbar("vert");
title(mytitle);
xlabel ("Winkel1")
ylabel ("Winkel2")
%axis tight
%set(gca,"xtick",[30 60 90 120 150 ])
%set(gca,"ytick",[30 60 90 120 150 ])
%Bildausgabe
bild1 =strcat("Kegel_",sprintf(field),".jpg")
bild2 =strcat("Kegel_",sprintf(field),".eps")
bild3 =strcat("Kegel_",sprintf(field),".pdf")
print ("-djpeg100",bild1)
set(gcf, "PaperPositionMode", "manual");
set(gcf, "PaperPosition", [0.5 0.5 8.0 8.0]);
print ("-depsc2", bild2);
print ("-dpdf", bild3);
p style="text-align:center;">